How To Find A Coterminal Angle Between 0 And 360
Find A COTERMINAL Angle Betwixt 0° AND 360°
1 consummate rotation of a ray in the anticlockwise direction results in an bending measuring of 360°.
By continuing the anticlockwise rotation, angles larger than 360° can be produced.
If nosotros rotate in clockwise direction, negative angles are produced. Angles 57°,417°and -303°accept the same initial side and terminal side merely with different amount of rotations, such angles are called coterminal angles.
Example :
For each given angle, observe a coterminal angle with measure of θ such that 0° ≤ θ< 360°.
(i) 395° (ii) 525° (iii) 1150°(iv) -270° (v) -450°
Solution :
(i) 395°
Write 395° in terms of 360°.
395° = 360° + 35°
Then, the coterminal angle of 395°is 35◦
(ii) 525°
Write 525°in terms of 360°.
525° = 360° + 165°
So, the coterminal angle of 525° is 165°.
(iii) 1150°
Write 1150° in terms of 360°.
1150° = 3(360°) + 70°
Then, the coterminal bending of 1150° is seventy°.
(iv) -270°
Write -270° in terms of 360°.
-270° = -360° + 90°
So, the coterminal angle of 270° is 90°.
(v) -450°
Write -450° in terms of 360 °.
-450° = -360° - xc°
And so, the coterminal angle of 450° is -90 °.
How to determine the quadrant of an angle ?
Positive Angle Quadrant :
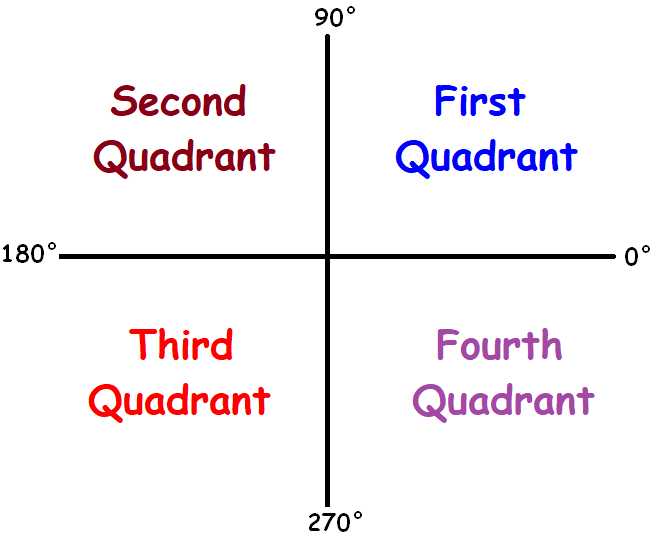
Angle lies betwixt 0° and 90 ° -----> onest quadrant
Bending lies between ninety° and 180° -----> twond quadrant
Angle lies betwixt 180° and 270 ° -----> 3rd quadrant
Bending lies between 270° and 360° -----> 2th quadrant
Negative Bending Quadrant :
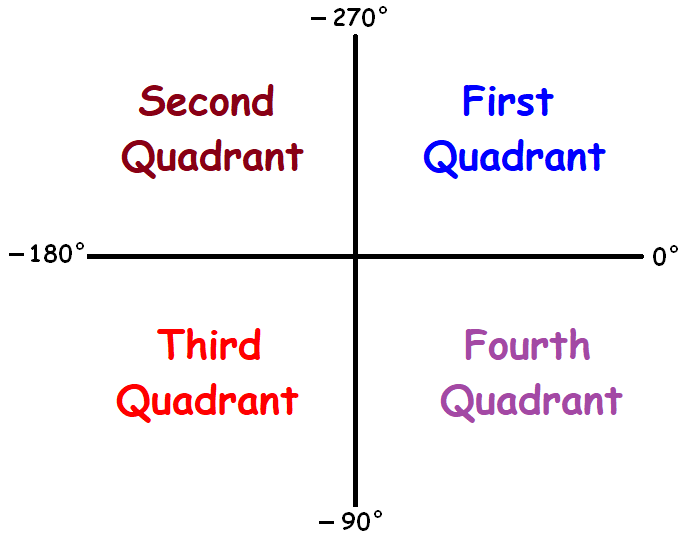
Bending lies between 0° and -90° -----> 4 thursday quadrant
Angle lies between -xc ° and -180 ° -----> 3rd quadrant
Angle lies between -180 ° and -270° -----> ii nd quadrant
Angle lies between -270° and -360 ° -----> onest quadrant
Example :
Identify the quadrant in which an angle of each given measure lies
(i) 25° (2) 825° (iii) −55°
Solution :
(i) 25 °
25 ° lies betwixt0° and 90°.
So, 25 ° lies in the first quadrant.
(2) 825°
If the given angle measures more 360°, then nosotros take to divide the given angle by 360 and find the quadrant for the remaining angle.
When 825° is divided by 360°, the remainder is 105°.
105° lies between 90 ° and 180 °.
So, 105 ° lies in the second quadrant.
(i) -55 °
-55 ° lies between -90 ° and 0°.
And so, -v5 ° lies in the fourth quadrant.

Apart from the stuff given in this section, if you lot need any other stuff in math, delight use our google custom search here.
Kindly post your feedback tov4formath@gmail.com
Nosotros always appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/find-a-coterminal-angle-between-0-and-360.html
Posted by: schuleroulk1944.blogspot.com


0 Response to "How To Find A Coterminal Angle Between 0 And 360"
Post a Comment