How To Find Surface Area Of Triangular Prism Formula
The surface area is the expanse that describes the fabric that will exist used to cover a geometric solid. When we decide the surface areas of a geometric solid we take the sum of the area for each geometric class within the solid.
The volume is a measure of how much a effigy can hold and is measured in cubic units. The volume tells u.s.a. something about the capacity of a figure.
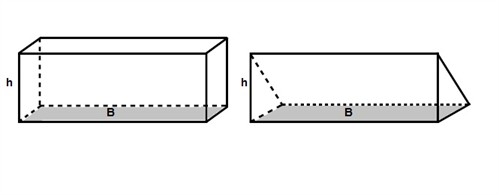
A prism is a solid effigy that has two parallel congruent sides that are called bases that are continued by the lateral faces that are parallelograms. There are both rectangular and triangular prisms.
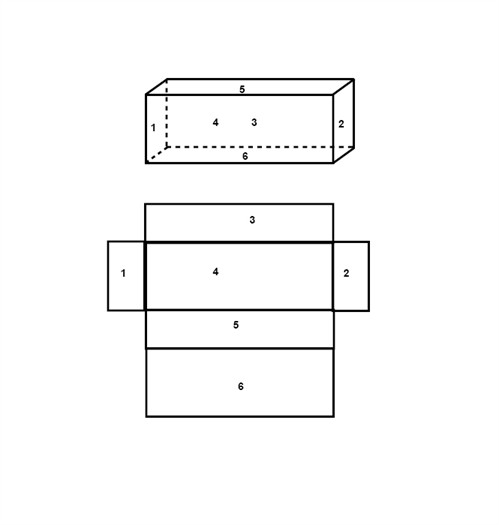
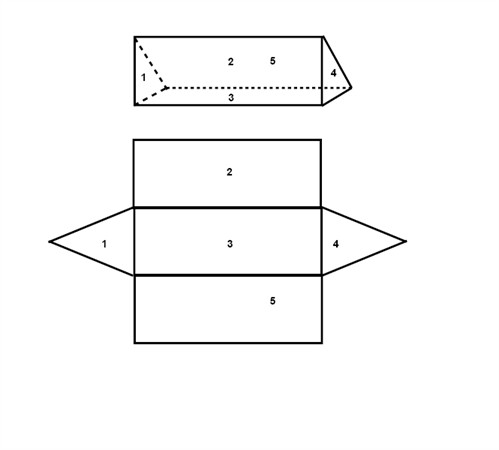
To find the surface area of a prism (or whatsoever other geometric solid) we open the solid like a carton box and flatten it out to find all included geometric forms.
To detect the book of a prism (information technology doesn't affair if it is rectangular or triangular) we multiply the surface area of the base of operations, called the base of operations area B, past the meridian h.
$$5=B\cdot h$$
A cylinder is a tube and is equanimous of two parallel coinciding circles and a rectangle which base of operations is the circumference of the circle.
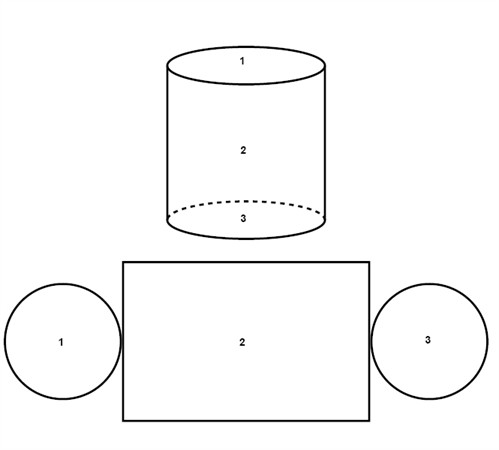
Example
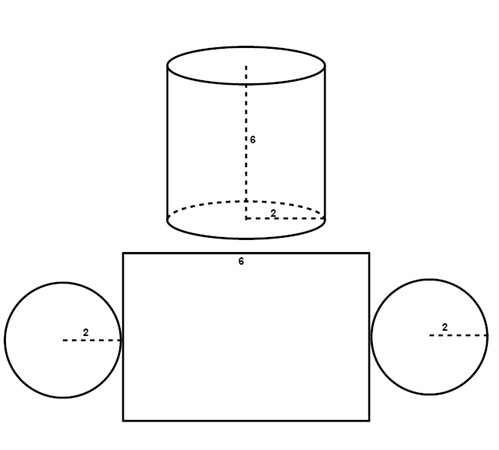
The surface area of 1 circumvolve is:
$$A=\pi r^{2}$$
$$A=\pi \cdot 2^{2}$$
$$A=\pi \cdot 4$$
$$A\approx 12.6$$
The circumference of a circle:
$$C=\pi d$$
$$C=\pi \cdot 4$$
$$C\approx 12.half-dozen$$
The area of the rectangle:
$$A=C\cdot h$$
$$A=12.6 \cdot 6$$
$$A\approx 75.6$$
The surface area of the whole cylinder:
$$A=75.6+12.vi+12.6=100.8\, units^{ii}$$
To observe the book of a cylinder we multiply the base of operations area (which is a circle) and the height h.
$$V=\pi r^{2}\cdot h$$
A pyramid consists of three or iv triangular lateral surfaces and a three or four sided surface, respectively, at its base. When we calculate the surface area of the pyramid beneath nosotros take the sum of the areas of the 4 triangles expanse and the base square. The height of a triangle inside a pyramid is called the slant superlative.
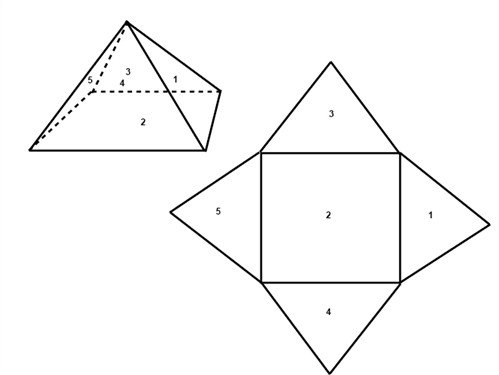
The book of a pyramid is one tertiary of the volume of a prism.
$$5=\frac{ane}{3}\cdot B\cdot h$$
The base of a cone is a circle and that is easy to see. The lateral surface of a cone is a parallelogram with a base that is half the circumference of the cone and with the camber elevation as the superlative. This tin can be a trivial bit trickier to encounter, but if you lot cutting the lateral surface of the cone into sections and lay them next to each other it's easily seen.
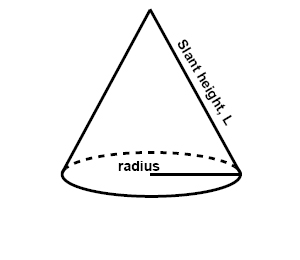
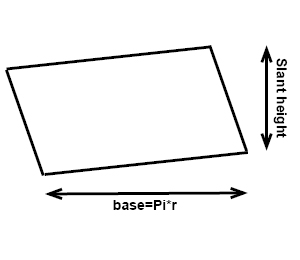
The surface surface area of a cone is thus the sum of the areas of the base and the lateral surface:
$$A_{base}=\pi r^{2}\: and\: A_{LS}=\pi rl$$
$$A=\pi r^{ii}+\pi rl$$
Example
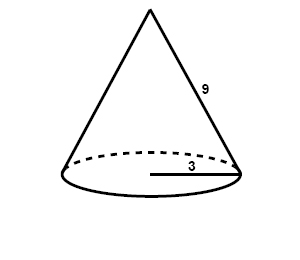
$$\begin{matrix} A_{base}=\pi r^{two}\: \: &\, \, and\, \, & A_{LS}=\pi rl\: \: \: \: \: \: \: \\ A_{base}=\pi \cdot 3^{ii} & & A_{LS}=\pi \cdot three\cdot 9\\ A_{base}\approx 28.3\: \: && A_{LS}\approx 84.8\: \: \: \: \: \\ \end{matrix}$$
$$A=\pi r^{2}+\pi rl=28.three+84.eight=113.i\, units^{2}$$
The volume of a cone is one third of the volume of a cylinder.
$$5=\frac{ane}{3}\pi \cdot r^{two}\cdot h$$
Example
Find the volume of a prism that has the base 5 and the height 3.
$$B=three\cdot 5=xv$$
$$5=15\cdot 3=45\: units^{iii}$$
Video lesson
Discover the surface area of a cylinder with the radius iv and height viii
Find the volume of a cone with top five and the radius 3
Source: https://www.mathplanet.com/education/geometry/area/the-surface-area-and-the-volume-of-pyramids-prisms-cylinders-and-cones
Posted by: schuleroulk1944.blogspot.com


0 Response to "How To Find Surface Area Of Triangular Prism Formula"
Post a Comment